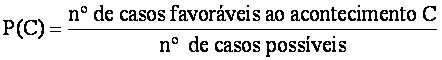PROBABILIDADES E ESTATÍSTICA

PROBABILIDADES E ESTATÍSTICA

1. TERMOS E CONCEITOS GERAIS

1.1. Experiências aleatórias e experiências deterministas

A palavra probabilidade, ou provável, usa-se em linguagem corrente quando queremos expressar a possibilidade de ocorrer determinado fenómeno.

- É provável que venha bom tempo…

- Tem boas probabilidades de ganhar o bingo…

Em matemática, quando falamos em probabilidades queremos referir-nos a um ramo da Matemática que estuda os fenómenos aleatórios.

Definição: Uma experiência é aleatória quando é impossível prever o resultado que se obtém, ainda que repetida nas mesmas condições.

Os fenómenos deterministas não interessam para o estudo das probabilidades.

Definição: Uma experiência é determinista quando é possível prever o resultado que se obtém se repetida nas mesmas condições.

Exemplos:

ALEATÓRIOS	DETERMINISTAS
Jogar e ganhar o totoloto	Atirar uma pedra ao ar e ver o que acontece
Concorrer e ganhar um concurso	Colocar dinheiro num banco e calcular o juro produzido num certo tempo
Atirar uma moeda ao ar e registar a face voltada para cima	Colocar dois produtos químicos em contacto e observar a reacção
Tirar uma carta de um baralho e registar a carta saída	Deixar de regar uma planta e ver o que acontece

1.2. Conjunto de resultados. Acontecimentos.

O rapa dos números

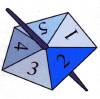
Suponhamos que realizávamos a seguinte experiência:

Rodávamos o rapa que está representado na figura e

anotávamos o número da face que ficou encostada à mesa.

Os resultados possíveis são 1, 2, 3, 4 e 5.

Ao conjunto chamamos espaço amostral ou conjunto de resultados.

A qualquer subconjunto de S chamamos acontecimento.

Aos subconjuntos constituídos por um só elemento chamamos acontecimentos elementares.

e são acontecimentos elementares

Aos subconjuntos com mais do que um elemento chamamos acontecimentos compostos.

e são acontecimentos compostos

Ao subconjunto chamamos acontecimento certo, pois coincide com o conjunto de resultados.

Ao conjunto chamamos acontecimento impossível.

Exemplo: Considera a experiência do lançamento de um dado com as faces numeradas de 1 a 6.

Define o conjunto de resultados.

Define e classifica o acontecimento:

A:”sair número par”;

B:”sair um número superior a 5”;

C:” sair um número menor que 7”;

D:” sair o número 7”.

Resolução:

(a)

(b) i) , acontecimento composto;

ii) , acontecimento elementar;

iii) , acontecimento certo;

iv) , acontecimento impossível.

EXERCÍCIOS

Observa as seguintes rodas da sorte:

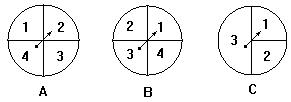
Se as seguintes afirmações são verdadeiras, indica a qual das roletas nos referimos:

É tão provável obter 2 como 3;

É mais provável obter 2 do que 3;

É menos provável obter dois do que 3.

2. Se tivermos um saco com 10 bolas brancas, 5 pretas e 5 azuis, e se tirarmos do saco uma bola ao acaso, podemos afirmar que:

- é mais provável tirar uma bola branca;

- é tão provável tirar uma bola preta como uma bola azul;

- é menos provável tirar uma bola preta do que tirar uma bola branca;

- é impossível tirar uma bola amarela;

- é certo tirar uma bola branca, azul ou preta.

Cria situações acerca das quais podes fazer afirmações em que utilizes as expressões:

- Muito provável; - Pouco provável; - Certo;

- Tão provável como; - Impossível.

3. Um cesto tem 10 laranjas, 8 peras e 5 maçãs. Tira-se ao acaso uma peça de fruta do cesto.

3.1. Qual é mais provável, sair uma laranja ou uma pêra?

3.2. Quantos elementos tem o conjunto dos resultados?

3.3. Classifica os seguintes acontecimentos:

a) A:” Tirar uma romã”. b) B:” Tirar uma maçã”.

4. A propósito do lançamento de uma moeda, indica:

a) o espaço amostral;

b) um acontecimento certo;

c) um acontecimento impossível.

5. Observa o gráfico seguinte que mostra as classificações de 0 a 20 de duas turmas do 9º ano, a Português.

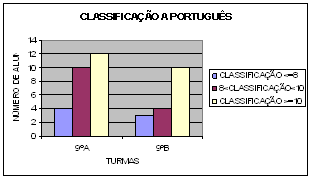
5.1. Encontramos um aluno do

9º A, aleatoriamente. Qual é a

classificação mais provável que o

aluno tenha tido a português?

E a menos provável?

5.2. Encontramos um aluno do

9ºB, aleatoriamente. Qual é a

classificação mais provável que o

aluno tenha tido a português? E a menos provável?

5.3. Quantos alunos tem a turma A? E a turma B?

6. Na experiência de lançar um dado, numerado de 1 a 6, e registar a face voltada para cima, consideraram-se vários acontecimentos.

Liga cada um dos indicados à classificação correspondente.

Acontecimento	Classificação
Sair um 3
Sair um número primo	Acontecimento elementar
Sair um 12	Acontecimento composto
Sair um número inferior ou igual a 6	Acontecimento certo
Sair 0	Acontecimento impossível
Sair 1 ou 3

7. Faz-se rodar a seta situada no centro do círculo. Ao parar, esta aponta para uma letra.

a) Indica qual o espaço amostral.

b) Dá exemplo de um acontecimento impossível.

c) Dá exemplo de dois acontecimentos elementares.

8. Uma experiência consiste em lançar um dado de doze faces idênticas, numeradas de 1 a 12 (dodecaedro regular),

e ver que face está voltada para cima. Indica:

a) O espaço amostral; b) O acontecimento : “Sair número par” ;

c) O acontecimento : “Sair face inferior a 8” ;

d) O acontecimento : “Sair face divisível por 2 e por 3” ;

e) O acontecimento : “Sair face superior a 12” .

9. Assinala com as letras P (possível), C (certo) e I (impossível) os seguintes acontecimentos:

Sair face 2 num dado de seis faces;

Um aluno da tua turma, escolhido ao acaso, ter menos de 2 anos;

A próxima semana ter pelo menos 5 dias.

Lei de Laplace. Determinação da probabilidade de um acontecimento.

Lei de Laplace

A probabilidade de um acontecimento C é o quociente entre o número de casos favoráveis ao acontecimento e o número de casos possíveis, ou seja,

Da definição de probabilidade conclui-se que:

A probabilidade do acontecimento certo é 1;

A probabilidade do acontecimento impossível é 0;

Exemplo:

Num cesto de fruta há 4 maçãs, 3 peras e 1 laranja.

Tira-se ao acaso uma peça de fruta. Calcula a probabilidade de ser:

a) Uma maçã: b) Uma pêra:

c) Uma laranja: d) Uma ameixa:

Esquemas auxiliares de contagem

A) Tabela de dupla entrada

(Só servem no caso de haver apenas dois objectos, ou então o mesmo objecto do qual se realizam duas experiências iguais consecutivas)

Lançaram-se dois dados numerados de 1 a 6.

a) Quantos são os acontecimentos elementares possíveis?

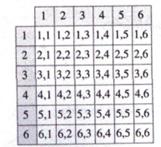
Vamos construir uma tabela.

Logo, temos 36 acontecimentos

possíveis.

b) Calcula a probabilidade de:

i) sair dois 5; ii) não sair 6;

Observando a tabela temos:

i) Casos favoráveis: 1 ii) Casos favoráveis: 25

Casos possíveis: 36 Casos possíveis: 36

Logo, Logo,

Exercícios

10. Considera a experiência de lançar uma vez o dado e anotar o número da face que fica voltada para cima. Determina a probabilidade de sair:

a) 5; b) um número par; c) 2 ou 3; d) não sair 4.

11. Numa caixa há 4 berlindes do mesmo tamanho mas de cores diferentes: 1 encarnado, 1 castanho, 1 verde e 1 amarelo.

a) Se se tirar um berlinde ao acaso qual é a probabilidade de sair verde?

b) O berlinde encarnado é substituído por um verde. Agora, qual é a probabilidade de tirar um berlinde ao acaso e sair verde?

c) Colocou-se mais um berlinde amarelo na caixa. Qual é a probabilidade de tirar um berlinde ao acaso e:

i) sair verde; ii) sair castanho; iii) sair preto;

iv) sair amarelo ou castanho; v) não sair verde.

12. De um baralho de 52 cartas retirou-se o 5 de copas e o 5 de ouros. A Joana baralhou as restantes cartas e tirou uma ao acaso. Qual é a probabilidade de:

a) sair uma carta de ouros; b) sair um 5; c) sair o 5 de ouros;

d)sair carta de copas; e) não sair carta de paus;

f) sair carta de espadas ou de paus;

g) sair uma carta vermelha ou uma figura (valete, dama ou rei).

13. Numa caixa há 4 berlindes azuis e 10 vermelhos. Um berlinde é tirado ao acaso. Qual é a probabilidade de sair:

a) um berlinde branco; b) um berlinde azul; c) não sair um berlinde azul?

14. Uma caixa contém 2 rebuçados de morango, 3 de ananás e 5 de limão. O Miguel tirou um rebuçado ao acaso e comeu-o. Em seguida voltou a tirar outro ao acaso.

a) O primeiro rebuçado era de limão. Qual é a probabilidade do segundo rebuçado ser também de limão?

b) O primeiro rebuçado não era de morango. Qual é a probabilidade do segundo rebuçado ser de morango?

15. Numa turma de 9º ano fez-se um inquérito cujos resultados estão registados na seguinte tabela de dupla entrada:

Pensa frequentar o 10º ano?	Sexo masculino	Sexo feminino
Sim	9	10
Não	6	3

Observando a tabela indica:

a) o número de alunos da turma;

b) quantos alunos pensam frequentar o 10º ano;

c) a probabilidade de, escolhendo um aluno ao acaso,

i) não ir frequentar o 10º ano;

ii) ser um rapaz que vai frequentar o 10º ano;

iii) ser uma rapariga que não vai frequentar o 10º ano.

16. O Pedro lançou um dado duas vezes seguidas.

a) Construa uma tabela de dupla entrada que mostre todos os casos possíveis;

b)Qual é a probabilidade:

i) de obter pelo menos um ás;

ii) de obter um 5 e um 3 por esta ordem;

iii) de obter a mesma pontuação nos dois dados;

iv) da soma das pontuações nos dois dados ser 8.

17) Num saco existem três bolas, uma branca, uma preta e uma cor de laranja. Extraem-se ao acaso e simultaneamente duas bolas do saco.

a) Quais são os acontecimentos elementares possíveis?

b) Qual é a probabilidade de:

i) sair a bola branca?

ii) não sair a bola preta?

18. Colocaram-se quatro cartões numa caixa, um com a letra A, outro com M, outro com O e o último com R. Extraíram-se simultaneamente dois dos cartões.

Qual é a probabilidade de obter uma das letras da palavra MO?

19. Lançámos duas vezes uma moeda. Qual a probabilidade de obter pelo menos uma vez face nacional?

20. Numa caixa existem 4 fichas numeradas de 1 a 4. Extraem-se ao acaso e simultaneamente duas fichas da caixa.

a) Quantos são os acontecimentos elementares possíveis?

b) Calcula a probabilidade de sair:

i) a ficha com o número 1 e a ficha com o número 3;

ii) uma ficha com um número par e a outra com um número ímpar;

iii) não sair a ficha com o número um.

B) Diagrama de árvore

(Servem para qualquer número de objectos)

Exemplo 1:

Lançaram-se três moedas (ou equivalentemente, lançou-se uma moeda três vezes consecutivas).

a) Quantos são os acontecimentos elementares possíveis?

Para contabilizarmos os casos possíveis vamos construir um diagrama de árvore:

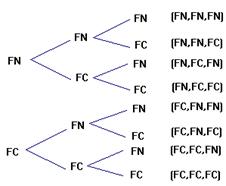
Logo temos 8 casos possíveis.

b) Calcula a probabilidade de saírem 2 vezes face comum.

As possibilidades que tempos de saírem duas vezes face comum são, (FN,FC,FC), (FC, FN,FC) e (FC, FC, FN). Logo os casos favoráveis são 3. Temos então

Exemplo 2:

Num saco há 5 rebuçados de café e 4 de morango. Um rebuçado é tirado ao acaso e, em seguida, sem repor o primeiro é tirado um 2º rebuçado.

Constrói o diagrama de árvore.

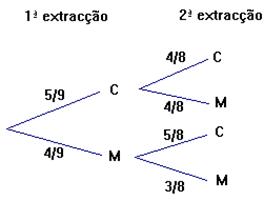
Probabilidade

b) Determina a probabilidade:

i) de nenhum dos rebuçados ser de morango;

ii) de apenas um ser de café.

Nota:

Como saber qual dos diagramas usar, se o do 1º ou o do 2º exemplo? Se reparares, no 1º exemplo, as três moedas são lançadas nas mesmas condições, ou seja, o lançamento da 2ª e 3ª moeda não é influenciado pelo lançamento da primeira. No entanto, no 2º exemplo isso já acontece, ou seja, o 1º lançamento influencia o 2º.

Conclui-se então que, em experiências em que se efectuam lançamentos, ou tiragens consecutivas, mas que existe reposição entre os lançamentos, usamos o diagrama do 1º exemplo. Já em experiências onde não seja feita reposição, usamos o diagrama do 2º exemplo.

Exercícios:

21. Considera a experiência de lançar uma moeda de 2 euros ao ar 3 vezes seguidas e anotar a face que fica voltada para cima.

a) Desenha um diagrama de árvore que mostre todos os casos possíveis;

b) Com o auxílio do diagrama anterior determina a probabilidade de obter,

i) só uma face nacional;

ii) pelo menos uma face nacional;

iii) nenhuma face nacional;

iv) só 2 faces nacionais.

22. Num saco há 2 berlindes brancos e 2 azuis. Um berlinde é tirado ao acaso e, em seguida, sem repor o primeiro é tirado um 2º berlinde. Determina a probabilidade de:

a) apenas um dos berlindes ser branco;

b) pelo menos um dos berlindes ser branco.

23. Um saco contém 8 bolas verdes e 4 amarelas. A Clara tira ao acaso 1 bola e anota a sua cor. Volta a repor no saco e agita-o para misturar bem as bolas. Tira novamente uma bola e anota a cor.

a) Desenha um diagrama de árvore que mostre todos os casos possíveis;

b) Calcula a probabilidade de ambas as bolas serem amarelas;

c) Qual a probabilidade de as 2 bolas serem de cores diferentes?

d) Qual a probabilidade de nenhuma bola ser verde?

24. O Tomás vai participar num torneio de ténis. Em cada jogo a probabilidade dele ganhar é e a probabilidade de empatar é .

a) Qual é a probabilidade dele perder?

b) Designando por G (ganhar), E (empatar) e P (perder) constrói o diagrama de árvore e determina a probabilidade do Tomás ganhar pelo menos 1 de dois jogos seguidos.

25. Numa gaveta há 4 meias brancas e 2 meias pretas. Tira-se da gaveta uma meia ao acaso e, em seguida, sem repor a primeira, é tirada uma segunda meia. Determina a probabilidade:

a) de as duas meias serem brancas;

b) de a primeira meia ser branca e de a segunda ser preta;

c) de ser uma meia de cada cor.

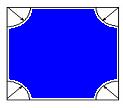26. Na figura está representado tampo de uma mesa,

quadrangular com 1 m de lado. Um ponto do tampo

da mesa é escolhido ao acaso. Calcula em percentagem

a probabilidade de se escolher um ponto da região colorida,

sabendo que o raio de um quarto de círculo é .

27. O Ricardo atira uma seta e acerta no alvo. Determina a probabilidade da seta acertar:

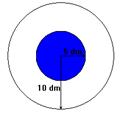
a) na região colorida;

b) na região não colorida.

28. Observa o quadro. Se fecharmos os olhos e escolhermos um ponto do quadrado ao acaso, qual é a probabilidade de escolher um ponto da região sombreada?

29. A Marta fez um inquérito a 300 sócios do Health Club que frequentava e obteve os seguintes resultados:

180 – praticam cardio-fitness (C)

100 – praticam musculação (M)

70 – só praticam natação (N)

a) De acordo com os dados obtidos preenche o seguinte diagrama, relativo aos 300 sócios inquiridos:

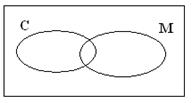
b) Qual é a probabilidade de escolher um dos inquiridos ao acaso e encontrar um que pratique:

i) musculação e cardio-fitness;

ii) só cardio-fitness;

iii) só natação ou só musculação.

30. O Tomás fez um inquérito aos 30 colegas da sua turma e concluiu que:

18 gostam de rock

9 gostam de rap

6 gostam de rock e rap

Os restantes não gostam nem de uma coisa nem de outra.

a) De acordo com os dados obtidos preenche o seguinte diagrama:

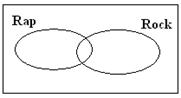
b) Determina a probabilidade de um aluno escolhido ao acaso entre os inquiridos:

i) gostar de Rap;

ii) gostar de Rap ou Rock;

iii) não gostar de nenhum dos estilos musicais.

31. Num jantar organizado pelos alunos de uma turma do 9º ano, perguntaram a todos os alunos que se inscreveram se queriam comer peixe ou carne.

7 só queriam comer peixe

6 só queriam comer carne

8 só queriam comer peixe e carne

9 eram vegetarianos e não queriam comer carne nem peixe

a) Preenche o seguinte diagrama;

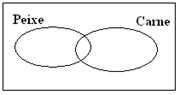
b) Calcula a probabilidade de escolher ao acaso, um dos participantes neste jantar e ele comer peixe;

c) Calcula a probabilidade de escolher ao acaso, um dos participantes neste jantar e ele não comer carne.

32. Um saco contém 3 bolas verdes e 2 encarnadas. Calcula a probabilidade de tirar em 3 extracções consecutivas, sem reposição:

a) três bolas verdes;

b) duas bolas encarnadas e uma verde;

c) pelo menos uma bola verde.

33. Um pacote contém 15 ursinhos cor de laranja, 13 amarelos e 12 verdes.

a) Tirando ao acaso um dos ursinhos qual é a probabilidade de:

i) sair laranja;

ii) não sair laranja;

iii) sair laranja ou verde;

b) Supõe que a Rita tirou dois ursinhos verdes e comeu-os. Qual é a probabilidade de ela tirar um terceiro ursinho ao acaso e ser:

i) amarelo;

ii) verde.

34. A turma da Isabel organizou um sorteio de um cabaz de Natal para angariar fundos para uma viagem de fim de curso. Venderam-se rifas azuis,

verdes e cor-de-rosa. A probabilidade da rifa vencedora ser azul é e de ser verde é . Qual é a probabilidade da rifa vencedora ser cor-de-rosa?

35. Numa caixa estão frascos de alperce, morango e laranja. Extrai-se ao acaso um frasco da caixa. A probabilidade de sair doce de alperce é e de sair doce de laranja é .

a) Determina a probabilidade de:

i) não tirar doce de alperce;

ii) tirar doce de morango;

b) Há 12 frascos de doce de morango. Quantos frascos há na caixa?